2017年7月の振り返り
どうも、パイソンです。
いつの間にか、7月も今日でおしまい。毎月の如く月の振り返りをしてみます。
7月の反省
一応、7月もRailsの勉強などを進めていく予定でした。
そして月初に書いてた通り、ブログもサボりグセをつけない用にしましょうという目標を立てておりましたが、、
結果全然更新を放置しておりました。。orz
まぁ、実際Railsで色々試して見たものの、わざわざブログにまとめる内容でも無いかもなー。。的な考えが先に働いて、ぐずぐず更新を放置してた結果、ずるずると月末まで来てしまったという次第であります。
どうもここ最近は、先に立てておいた目標に対して行動が伴っていない。
端的に言えば、言った事をやらないという、あまり宜しく無い状態になっているのは反省すべきですな。
次月以降に向けて
4月にブログを始めてからというもの、月単位で目標管理的な記事を書いてましたが、ちょっと今後数ヶ月はこういうことを書くのは控えておこうかと。
なんか、自分で自分のクビを絞めてる感が半端無い上に義務感でブログとか書いててもシンドイだけやしなー。(´д`)
仕事で書いてるんじゃあるまいし。。ブツブツ
というわけで、今回は単なる愚痴ブログにしかなってません。<(_ _)>
また気が向いたらボチボチ更新することにしますわ。
ではでは。
2017年7月の目標
どうも、パイソンです。
本日から7月。いやー、もう1年の折り返し地点ですなー。
感覚的には、年明けを迎えたのがつい最近のことに思えてしまうのですが、時が過ぎてしまうのは本当にあっという間だという感じがします。
それはさておき、7月の目標をサクッと書いておきます。ま、こういうのも早めにやっておかないとズルズルと時間だけが過ぎ去ってしまいますんで。
Railsの勉強
先月、環境構築までは出来たRailsですが、もう少し深く勉強して見たいところ。
目先やりたい事としては、Herokuの環境周りの勉強と、Railsで何か作って見るかなーという感じです。
具体的にやろうと決めてることとしては、
という感じです。
記事更新回数
ま、先月が5回程度だったので、今月はそれより多く更新します。
つか、一度更新をサボり気味にするとクセがついて、1週間ぐらい平気で放置しちまうからなー。。(´д`)
少し更新グセをつける行動をしておきたいと思います。
とゆーわけで、今月は頑張るぞー。
ブログ3ヶ月目の振り返り
どうも、パイソンです。
早いもので、ブログ開始からもう3ヶ月目。毎月の如く今月の振り返りをします。
6月の目標
一応、6月はRailsの勉強を目標にしておりました。
記事更新
今月は、Railsの記事とCodeIQの記事とで実質3記事の更新。うーん、ちょいと少ないなー。これは明らかに反省材料。
ちなみに、この記事を書くときに先月自分が書いた記事を見てみたら、、
1ヶ月は長いようで、気が付けばあっという間に過ぎ去ってしまうもの。次月以降は計画的に更新していけるように頑張ります。
http://osishow3.hateblo.jp/entry/2017/05/31/235500
おい!どの口が言った!!?
まとめ
色々と反省材料の多い6月でした。が、過ぎ去った事をあれこれ考えても致し方無し。
というわけで、
来月から頑張ります!(`・ω・´)
ではでは。
herokuでRailsアプリを動かしてみた
どうも、パイソンです。
前回の記事では、Windows環境で簡単なRailsアプリを動作させたときの手順を解説しました。
今回の記事は、作成したRailsアプリをHerokuで公開した時の手順のメモになります。
Herokuアカウントの作成
先ずはHerokuにアクセスしてユーザー登録を行います。
トップページから、[SIGN UP FOR FREE]のリンクをクリック。
その後は画面の指示に従い、アカウント登録を行います。
Heroku CLIのインストール
アカウント登録が完了したら、Heroku CLIをインストールします。
こちらは、PCからHerokuサーバへのコマンド実行をする為のツールになります。
以下のリンクから、32-bitまたは64-bitのインストーラーをダウンロードして、実行します。
https://devcenter.heroku.com/articles/heroku-cli#windows
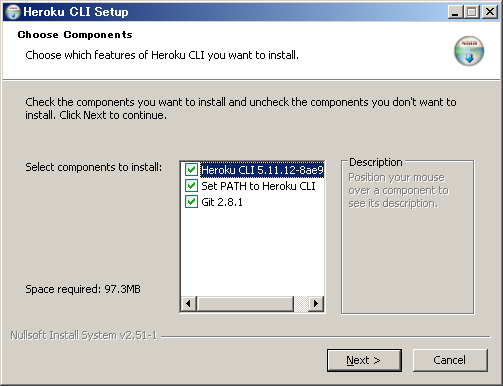
実行後、上のようなダイアログが表示されます。
このインストーラーではHeroku CLIだけでなく、Gitのインストーラーも兼ねているようですね。
Gitのインストール
Heroku CLIのインストールが終わると、次にGitのインストールが始まります。
Gitのインストール時の選択項目は少しデフォルトと異なる設定にしました。
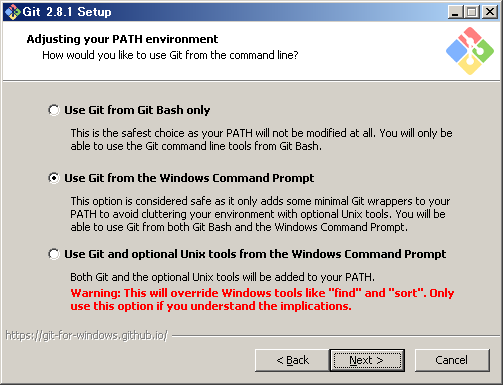
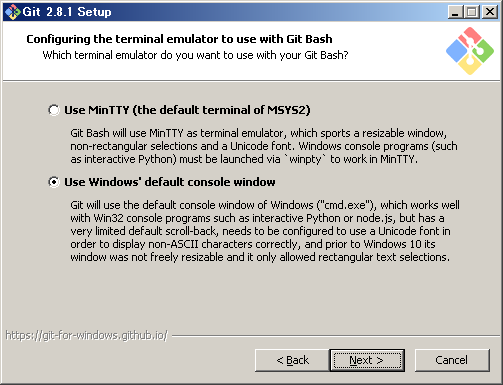
こちらのダイアログでは、Windowsのコマンドプロンプトからgitコマンドが実行できる様に、「Use Git from the Windows Command Prompt」を選択しました。
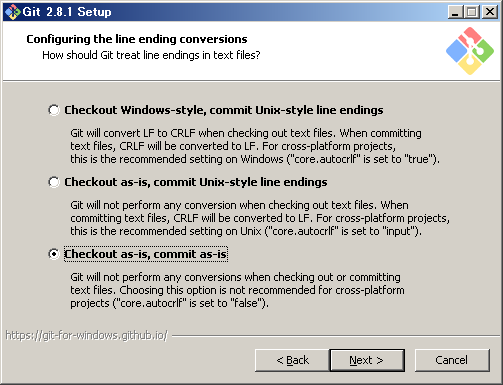
また、こちらのダイアログでは、「Checkout as-is, commit as-is」を選択しました。
これは、WindowsとUnix環境では改行コードの扱いが異なるのですが、Gitでファイルを転送する度に改行コードを変換されるのが煩わしいという個人的な理由からです。
インストール確認
上記のインストール作業完了後、コマンドプロンプトを起動して、herokuコマンドとgitコマンドが問題なく動作すればインストールは成功です。
>heroku --version heroku-cli/5.11.12-8ae9780 (windows-amd64) go1.7.5 >git --version git version 2.8.1.windows.1
Railsアプリケーションの設定
Herokuに公開するにあたり、データベースとしてpostgresqlを使う為の設定を行います。
(サンプルアプリなのでsqliteでも良い問題無いかもしれませんが、その辺は今回検証しておりません。)
前回の記事で作成したRailsアプリ内のファイルを編集します。
Gemfileの編集
RailsアプリではGemfileというファイルに、アプリの動作に必要なライブラリが記載されています。ここに、Postgresqlモジュールの定義を追加します。
変更前
gem 'sqlite3'
変更後
gem 'sqlite3', group: :development # Use postgresql as the database for Active Record in production gem 'pg', group: :production
上記の書き方で、development環境ではsqlite3、production環境ではpostgresqlを利用するようになります。
config/database.ymlの編集
データベース定義であるdatabase.ymlを以下のように編集します。
変更前
production: <<: *default database: db/production.sqlite3
変更後
production: <<: *default adapter: postgresql encoding: unicode pool: 5
これで、production環境でのデータベースをpostgresqlに設定出来ました。
この作業が完了したら、コマンドプロンプトを起動し、Railsアプリのフォルダまで移動後、以下のコマンドでGemfileに追加したモジュールのインストールを行います。
>bundle install
Railsアプリケーションのデプロイ
ここから、Herokuへのアプリケーションのデプロイを行っていきます。コマンドプロンプトを起動し、以下のコマンドを順次実行していきます。
>heroku login
先ずはloginコマンドを実行します。認証情報が要求されるので、アカウント登録時のメールアドレスとパスワードを入力してログインします。
>heroku create
次に、createコマンドを実行します。これはHeroku上にアプリケーションを登録するコマンドになります。実行すると以下の様な出力が表示されます。
Creating app... done, <アプリケーション名> https://<アプリケーション名>.herokuapp.com/ | https://git.heroku.com/<アプリケーション名>.git
今回はcreateの後ろに何も入力していませんので、アプリケーション名はHeroku側が自動で決めてくれます。
因みに、自分でアプリケーション名を付けたい場合は、createの後ろにアプリケーション名を指定しましょう。但し、アプリケーション名はHeroku上で一意である必要があります。
アプリケーションの登録後、ローカルのRailsアプリ上でGitのリポジトリを作成し、Heroku側にpushします。コマンドプロンプトからRailsアプリのフォルダまで移動した後、以下のコマンドを順次実行します。
> git init > heroku git:remote -a <アプリケーション名> > git add --all > git commit -m "initial commit" > git push heroku master
git pushまで実行すると、Heroku上でアプリケーションのデプロイが行われます。
補足
因みに、heroku createコマンドをRailsアプリのフォルダ上で実行した場合はgitリポジトリの設定もしてくれるようで、
> git init > heroku git:remote -a <アプリケーション名>
の2つの実行が省略出来るようです。
デプロイに失敗する場合
この時、もし最後のデプロイに失敗したらコンソール出力に以下のようなメッセージが出てしまいます。
error: failed to push some refs to 'https://git.heroku.com/<アプリケーション名>.git'
Gemfileかdatabase.ymlに問題がある可能性が高いですが、別の原因の場合はコマンドプロンプトのエラー出力から原因を追うしかありません。
Railsアプリケーションのマイグレーション
デプロイ後、データベースのマイグレーション処理を行います。以下のコマンドを実行します。
heroku run rake db:migrate
マイグレーション後、ブラウザからアプリケーションにアクセスします。
https://<アプリケーション名>.herokuapp.com/blogs
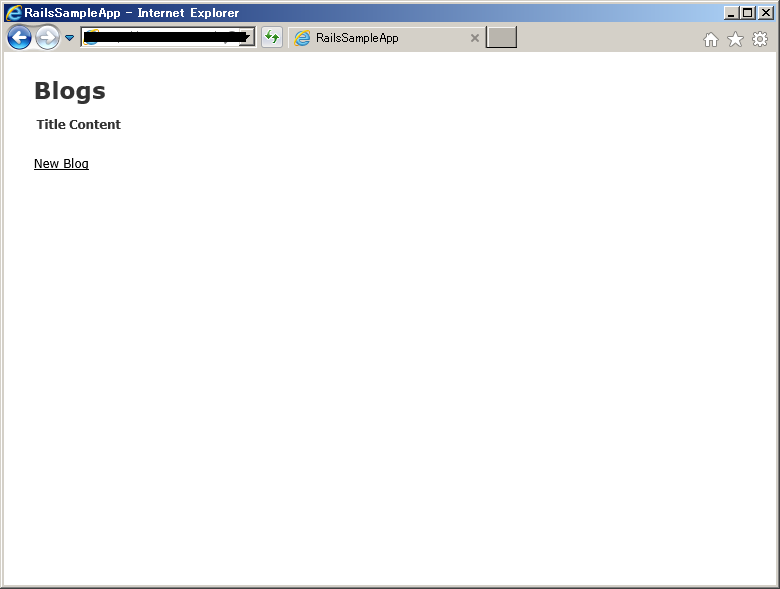
アプリが起動し、データ登録が問題なく出来れば完了です。
マイグレーションに失敗する場合
ブラウザでアクセスしてもエラーメッセージが表示される場合は、マイグレーションに失敗している可能性があります。
コマンドプロンプト上に下記の様なメッセージが表示されているかもしれません。
PG::ConnectionBad: could not connect to server: No such file or directory
このエラーが表示される場合は、Heroku上のアプリケーションにPostgresqlのアドオンが登録されていない可能性があります。
>heroku addons:add heroku-postgresql
上記コマンドでアドオン登録を行った後、再度マイグレーション処理を実行すると、問題が解決する事があります。
参考:Heroku上からのアプリケーションの削除
ここまでで、Heroku上にアプリケーションを公開するところまで行いました。
今回登録したアプリケーションは、インターネット上に公開され、URLさえ解れば誰でもアクセスできる状態にあります。
ま、誰かがアクセスして来たとしても実害はあることは無いでしょうが、公開されたままの状態が気持ち悪いという場合は、以下のコマンドでアプリケーションを削除しておきましょう。
heroku apps:destroy --app <アプリケーション名>
Windows環境でRailsを動かしてみた
どうも、パイソンです。
とりあえず今月からRailsの勉強を始めようかということで、いろんなWebページやら本などに目を通しておりました。
そして、この度やっとこさ自分のPCでRailsアプリを動作させる所までできたので環境設定手順をここにメモしておこうと思います。
因みに、OSはWindows7 Home Premium 64bit の環境で検証しています。
環境設定手順
Rubyのインストール
まずはRubyInstaller 2.4でRubyのインストールを行います。
https://rubyinstaller.org/downloads
因みに、私のPC環境は64bitなので[Ruby 2.4.1-1 (x64)]をダウンロードしました。

Installerを起動して利用条件に同意した後、インストール場所とオプションを選択します。デフォルトでは、上から1番目と2番目にチェックが付いていましたが、私の場合は1番目と3番目のチェックをつけてインストールを実行しました。

インストール完了画面で、「Run 'ridk install'...」という項目にチェックをつけたままFinishをクリックします。

MSYS2等をインストールするコンソールメニュー画面が立ち上がります。
1->2->3と上から入力していけば順次インストールが実行されます。
最後にコマンドプロンプトを立ち上げて、rubyがインストールされたことを確認します。
>ruby -v ruby 2.4.1p111 (2017-03-22 revision 58053) [x64-mingw32]
Railsのインストール
引き続き、コマンドプロンプトからrailsのインストールを行います。
>gem install rails
完了後、railsのバージョン確認を行います。
>rails -v Rails 5.1.1
また、railsアプリで使用するデータベースとしてsqlite3をインストールします。
gem install sqlite3
sqlite3がインストールされたことを確認します。
>gem list sqlite3 *** LOCAL GEMS *** sqlite3 (1.3.13 x64-mingw32)
Node.jsのインストール
Node.jsをインストールします。後に作成するrailsアプリの動作に必要となります。
https://nodejs.org/en/download/
環境設定は以上です。
Railsアプリケーションの作成
環境設定が完了したら、Railsアプリケーションの作成をします。
アプリケーションを作成するには、railsのコマンドを実行するだけです。非常に簡単ですね。
コマンドプロンプトからrailsのアプリを生成するフォルダまで移動した後、以下のコマンドを実行します。
>rails new rails-sample-app >cd rails-sample-app >rails s
実行後、http://localhost:3000/にアクセスして、“Yay! You're on Rails!”の画面が表示されたら成功です。

scaffoldを使ってデータベース更新機能を追加する
scaffoldとはRailsが提供する機能の一つで、データの更新、削除など一通りの機能のテンプレートを生成してくれます。
コマンドプロンプトから先ほど作成したRailsアプリケーションのフォルダ配下で、以下のコマンドを実行します。
> rails g scaffold Blog title content:text > rails db:migrate > rails s
実行後、http://localhost:3000/blogsにアクセスして、以下のようなメニュー画面が表示されたら成功です。

ブラウザから、データの作成、更新、削除が出来るか試して見ましょう。
CodeIQ 「タンジェント・フラクション」問題解答コード
CodeIQ問題の解答公開記事です。
codeiq.jp
問題の概要
今回は以下のような問題でした。
方針
この問題を解くためには、以下の三角関数の公式を使います。
題意から、はそれぞれ単位分数となるので、
を自然数とした時に、それぞれ
とあらわす事が出来ます。これを先の公式に当てはめると、
となります。
というわけで、を満たし、且つ右辺が単位分数になるような自然数
の組み合わせの数を算出すれば良いと言う事になります。
解答コード
こちらが提出したコードになります。
class Codeiq3182 def solve(m) cnt = 0 tan_m = Math.tan(m) max_b = (1 / Math.tan( m / 2.0 )).to_i (2..max_b).each do |b| i=((b**2 -1).to_f / (2 * b).to_f).ceil (i..(b-1)).each do |n| (a, r) = ((n*b) + 1).divmod(b-n) next if (r != 0) tan_ab = (a + b).to_f / ((a * b) -1) break if(tan_ab < tan_m) cnt += 1 end end return cnt end end puts Codeiq3182.new.solve(gets.to_f)
が単位分数になるので、
を自然数とした時に
が成り立つ自然数
の組を求める方法で解いています。
上記の式を組み変えると、になるので、右辺を実際に計算して余り0になる
の組み合わせの数をカウントしてます。
の値を定義した時、
の値が計算上1以上になるように
の初期値を調整しているのが、工夫といえば工夫なのかもしれません。
感想とか
三角関数とか使うのは学生時代以来なので、最初は問題の内容を理解するだけでいっぱいいっぱいでした(><)
記事ではさらっとの公式を書いていますが、実際はかなり数学の解説サイトをググって調べてきたものです。もはやこのへんの公式とかは、頭の中からすっぽり抜け落ちてしまってますなー。。
また、今回の解法もかなりしらみつぶし的なやり方で解いているので、もう少し効率の良いやり方があるのかと色々考えては見ましたが、現状ではこれが精一杯ですw
実行速度は、まだまだ改善の余地はありそうですね。
2017年6月の目標
どうも、パイソンです。
気が付けば、もう6月も7日目。先月は月中から月末にかけて記事を書いてきた跳ね返りか、1週間程ブログを放置しておりました。
しかし、このままずるずるとしてると今月は何もしないまま過ぎ去ってしまいそうなので、ここいらで6月の目標を書いてみようかと思います。